Corona & Üssel Artış – Corona Hangi Hızda Yayılıyor? Günlük hayat içinde sıklıkla duyduğumuz matematik terimleri vardır. Özellikle artış miktarı bildirmemiz gerektiğinde ve özellikle büyük miktarda artış ise matematiksel bir dil kullanmaktan başka bir yolumuz yok demektir. Bu durum birçok defa duyduğumuz matematik bir dildir ifadesinin önemini anlamamızı sağlıyor.
Son günlerimizin mutlak gündemi olan Covid-19 virüsü ve pandemi ile TV’den ve sosyal medyadan hastalığın yayılma hızıyla ilgili sayısal verileri takip ediyoruz. Bu gündem içinde yine sıklıkla duyduğumuz “Üssel Artış” ifadesi, acaba ne demektir? şeklinde düşünmemizi sağlıyordur.
Corona & Üssel Artış
Gelin, bugün bu “Üssel Artış” meselesini açıklığa kavuşturalım;
Öncelikle kıyaslayabilmek için “Doğrusal Artış”ın ne olduğunu anlayalım ve sonra da iki artış miktarı arasındaki farkları yorumlayalım.
Matematik doğrusal olmayı “ax + b” şeklinde ifade etmektedir (a ve b’yi şimdiye kadar öğrendiğiniz sayılar olarak düşünebilirsiniz). Hatta bu tür ifadelere “Lineer denklemler” de denilmektedir. Bu doğrusal ifadenin bir de şekli, daha doğrusu grafiği vardır. İnsan hafızası şekilleri daha iyi tutabildiği için şekillerden faydalanmak öğrenme için son derece gereklidir. Bu nedenle doğrusal ifadeyi, iki reel sayı ekseninin dik kesişmesinden oluşan koordinat ekseninde göstermek için noktalardan oluşan bir yapıya dönüştürmeliyiz.
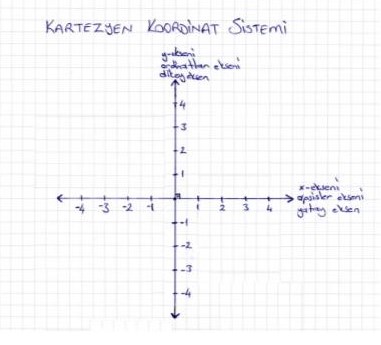
Eksende dikey eksen “y” ekseni, yatay eksen ise “x” ekseni olarak adlandırılır. “x” ekseni Reel sayılar ekseni olarak da sıklıkla kullanılır. Örneğin 2 rakamını eksende göstermek istediğimizde yerini bulmak son derece kolaydır.
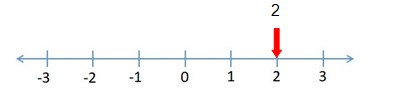
Benzer şekilde 3/2 kesrini de kolayca gösterebiliriz (Yer bildiren okun 1 ve 2’nin tam ortasında olduğu kabul edilmiştir).
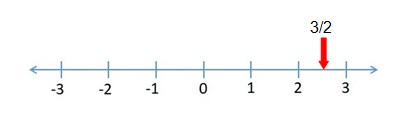
Aynı şekilde = 2,23606….. sayısını da gösterebiliriz (Eksende 2 ve 3 arası on eşit parçaya bölünmüş ve sayısı, 2.ve 3. parça arasına yerleştirilmiştir).
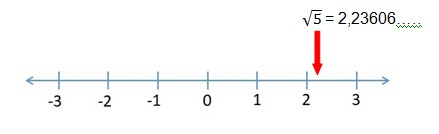
Eğer reel sayı ekseninde göstermek istediğiniz sayılar negatif sayılar ise bu defa aynı işlemi sıfırın solunda yapmanız gerekecektir. Bir boyutlu olarak ifade edilen reel eksende sayıları göstermek kısmen daha kolaydır.
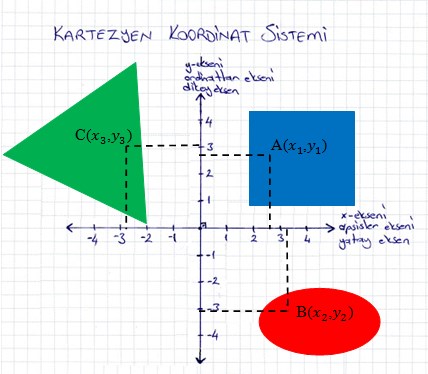
Kartezyen Koordinat Sistemi
Bu arada yine sıklıkla duyduğumuz kavramının ne olduğuna yeri gelmişken değinmekte fayda olacaktır. Boyut, uzayda belirtmek istediğimiz şey için gereken minimum koordinat sayısıdır. Örneğin iki boyutlu olarak (x,y) ikililerden bahsettiğimiz gibi en – boy gibi daha iyi bildiğimiz kavramları da kastediyor olabileceğiz.
Az önce sayı ekseninde gösterdiğimiz rakam ve sayılar bir boyutlu bir eksen üzerindedir. Çünkü sayıları belirtmek için sadece bir koordinat yeterliydi. Ancak (x,y) gibi ikilileri tek bir sayı ekseninde gösteremeyiz. Bu nedenle bir reel sayı eksenine daha ihtiyaç duyarız. Bu nedenle de yazının başlarında gösterdiğim reel sayı eksenlerinin dik kesişmesinden oluşan bir koordinat ekseni oluşturulmuştur. Bu eksen iki boyutludur. Çünkü eksen üzerinde her hangi bir şeyin yerini göstermek için iki koordinat gereklidir x ve y gibi. (x,y) ikilisinin yerini göstermek için önce ilk yazılan sayı yatay eksen üzerinden bulunur ve ardından ikinci sayı dikey eksen üzerinde belirlenir. Ardından belirlenen noktalardan eksenlere paralel çizgiler çekilir ve çizgilerin dik kesiştiği köşe (x,y) ikilisinin yeri olur.
Örnek olarak, A(1,2), B(-1,1), C(-2,-3), D(4,-2) noktalarını eksende gösterelim.
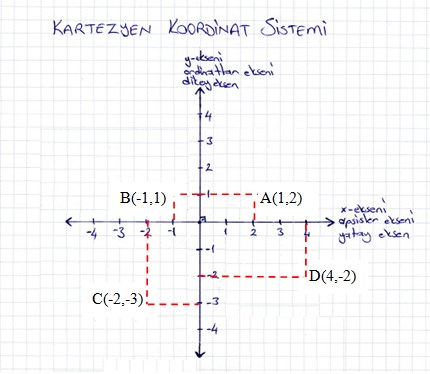
Bu gösterimleri yapabilmekte son derece kolaydır.
Geometrik Şekiller
Kare, üçgen gibi şekillerin neden iki boyutlu olarak adlandırıldığı artık daha net anlaşılmış olmalıdır. Aşağıda verdiğim eksen üzerindeki gösterime de bakmak da faydalı olacaktır.
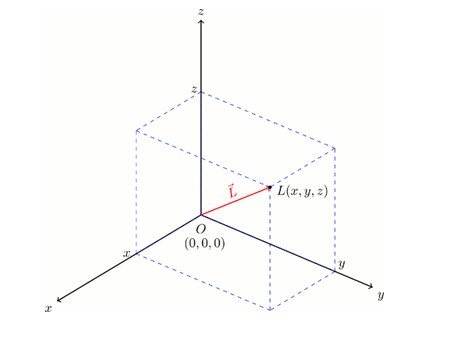
Ancak Silindir, Küp gibi nesneleri ifade etmek için iki koordinat yetmeyecektir. Çünkü bu nesneler uzayda bir en, boy ve yüksekliğe sahiplerdir. Aşağıdaki gösterim anlatmak istediğimi özetlemektedir.
Boyut konusuna biraz değindikten sonra doğrusal artışın nasıl olacağını gösterebiliriz.
Doğrusal Artış
Doğrunun “ax+b” şeklinde ifade edildiğini görmüştük. Doğrusal artışı anlamanın en kolay yolu koordinat ekseninde belirttiği grafiği görmektir. Koordinat ekseninde gösterim için bir “x” ve bir “y” bileşenine ihtiyacımız olacaktır. Bu nedenle doğrusal ifademizi “y” ye eşitleyebiliriz;
“y = ax+b” eşitliğiyle ihtiyacımız olan iki değere de ulaşabileceğiz.
Örnek olarak, y = 2x+1 eşitliğiyle ihtiyacımız olan her iki değeri de bulabiliriz. Bunun için x’e bazı değerler vererek y’nin aldığı değerleri bulabilir ve bulduğumuz değerleri koordinat ekseninde gösterebiliriz.
X = 0 için; y = 2.0 – 4 = -4 (0,-4)
X = 1 için; y = 2.1 – 4 = -2 (1,-2)
X = 2 için; y = 2.2 – 4 = -0 (2,0)
X = 3 için; y = 2.3 – 4 = 2 (3,2)
X = 4 için; y = 2.4 – 4 = 4 (4,4)
X = 5 için; y = 2.5 – 4 = 6 (5,6)
Noktaları koordinat ekseni üzerinde gösterdiğimiz de doğrunun grafiğini ve artış miktarını görmüş olacağız. Ancak öncesinde yukarıdaki değerleri incelediğimizde x’lerin her 1 birimlik artışının y’nin değerini 2 birim arttırdığını görüyoruz. Ayrıca bu artış miktarının x’in değerlerinin değişiminden etkilenmediğini anlıyoruz. Bu sabit artış miktarlı büyümeye “Doğrusal Artış” denir. Şimdi grafiğimizi çizebiliriz;
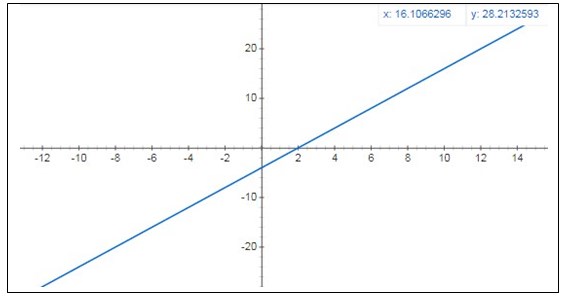
Doğrusal artışın birim miktar değişimlerde sabit miktarda artış olduğunu anlamış bulunuyoruz. Şimdi “Üssel Artışı” ın ne olduğunu anlamaya çalışalım;
Üssel Artış
Matematikte üslü ifade dendiğinde, bahsedilen sembolün sağ üst köşesinde sayı veya sembollerin olduğu anlaşılır (Bu arada yazımızda geçen reel sayılar, üslü sayılar gibi sayı kümelerinin gerekli aksiyom, tanım ve teorilerle kanıtlandığı kabul edilmiştir. Aksi durumda gerekli yapının kurulması bir ders kitabı olabilecek uzunlukta olacaktır). Aşağıda üslü ifade örnekleri verilmiştir;
xx = x.x.x……x ; x üssü x şeklinde okunan ifade, x’in x defa çarpılacağı anlamına gelir.
23 = 2.2.2 ifadesi 2 üssü 3 diye okunur ve 2’yi 3 defa çarpmamız gerektiğini bildirir.
23 = 8, benzer mantıkla bu üslü sayının eşitinin 8 olduğunu kolayca buluruz.
Şimdi üslü arştı anlayabilmek için yine koordinat ekseninde gösterebileceğimiz bir eşitlik oluşturalım;
Koordinat ekseni için bir x ve bir y’ye ihtiyacımız olduğunu artık biliyoruz. Bunu üslü bir ifade şeklinde oluşturmalıyız.
“y = Ax” Grafiği
y = 3x şeklinde bir eşitlik yazalım. Bu defa yine üssel artışın nasıl olduğunu anlayabilmek için x’e verdiğimiz bazı değerlere karşın y’nin aldığı değerleri yazalım;
x = 0 için y = 30 = 1 ; (sıfırıncı kuvvetin 1 e eşit olduğu kabul edilir)
x = 1 için y = 31 = 3 ; (3’ün kendisi)
x = 2 için y = 32 = 9 ; (3.3 = 9)
x = 3 için y = 33 = 27 ; (3.3.3 = 27)
x = 4 için y = 34 = 81 ; (3.3.3.3 = 81)
x = 5 için y = 35 = 243 ; (3.3.3.3.3 = 243)
Yukarıdaki x’in her bir birimlik değişimine karşın y’nin artış miktarının sabit olmadığı görülüyor. X’in ilk bir birimlik artışında y, 2 birim artarken x’in ikinci bir birimlik artışında bu defa y, 6 birim artmıştır. Y’nin bir sonraki artış miktarı 18 birim, sonraki artışı 54 birim olmuştur. Bu artış miktarında sabit bir artış miktarı yoktur, sabit bir artış oranı vardır. Her bir artış miktarında y’nin ulaştığı değerlerin oranlarının sabit olduğunu görebiliriz; 1/3 = 3/9 = 9/27 = 27/81 = 81/243
Yine üslü artışı tam görebilmemiz için y = 3x eşitliğini grafik olarak da gösterelim;
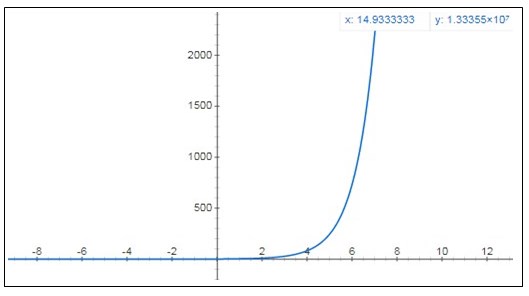
(Bu üssel artış grafiğinin corona artış grafiğine olan benzerliği dikkatinizden kaçmamıştır.)
Üssel Artış – Corona Hangi Hızda Yayılıyor?
Artık her iki artışın nasıl olduğunu biliyoruz. Corona artışının hangi atış biçimine göre gerçekleştiğini sezgilerimizin dışında sayısal olarak da görebiliriz. Bunun için öncelikle hastalığın nasıl yayıldığı ile ilgili bir modelimiz olmalıdır. Öncelikle ilk Hasta sayımızı H0 ile ifade edelim ve her hastanın bir günde x kişiye hastalığı bulaştırdığını kabul edelim. Bu yayılma modeliyle hastalığın nasıl yayıldığına bakalım (Birinci gün hasta sayısını H1 ile ikinci gün H2 ile ve devam eden günler benzer numaralandırma mantığı ile gösterilecektir);
İlk gün H0 var ve H0.x kişiye de bulaştırdığını kabul ettiğimizden ilk ; H1 = H0 + H0.x hasta olacaktır. 1.Gün hasta sayımızı; H1 = H0 + H0.x , şeklinde ifade edebiliriz. 2.Gün H1 olan hasta sayısına ve H1.x yeni enfekte olan kişiyi de eklediğimiz de hasta sayısı, H2 = H1 + H1.x olacaktır. H1 yerine, H0 + H0.x yazdığımızda;
H2 = H0 + H0.x + (H0 + H0.x)x = (H0 + H0.x)(1+x) = H0 (1+x)(1+x)
H2 = H0(1 + x)2 olacaktır. Benzer şeklide diğer günleri de yazdığınızda şu şeklide bir artış ortaya çıkacaktır;
1.Gün; = H1 = H0(1 + x)1
2.Gün; = H2 = H0(1 + x)2
3.Gün; = H3 = H0(1 + x)3
4.Gün; = H4 = H0(1 + x)4
.
.
n.Gün; = Hn = H0(1 + x)n
Modelleme – Corona Hangi Hızda Yayılıyor?
Hastalığın yayılma modelinde her gün yaşanacak artışın ilk hasta sayısının (1+x)’in gün sayısı kuvvetiyle çarpılmasında elde edilebileceği görülüyor. Model üslü bir ifadeyi içerdiğinde hastalık üssel bir şekilde artacaktır (Ancak enfekte olmuş kişiyle karşılaşan kişi sayısı ve bağışıklık gibi birçok faktör bu modelde ihmal edildiğinden artış bu denli sabit oranla gerçekleşmeyecektir).
Günlük hasta sayısını bulabilmenin yanında virüsün yayılma hızını da hesaplayabiliriz. Virüsün yayılma hızını vy ile ifade edelim. vy, burada ihmal edilen diğer değişkenlerin dışında kişi / kişilerin karşılaştıkları kişi sayısına ve bulaşma oranının çarpımına da bağlıdır. Yayılma hızını şöyle ifade edebiliriz;
vy = = i.b (i: enfekte olan kişiyle karşılaşan kişi sayısı, b: hastalığın bulaşma oranı
Örneğin bulaşma oranı 0.01 olduğu bir salgında hasta olan kişi günde 100 kişiyle karşılaşırsa ve her karşılaştığı kişiye de bulaştırdığını kabul edersek o gün 1 kişiye daha hastalık bulaşır. Her gün 1000 kişiyle karşılaşırsa 10 yeni hasta, 10.000 kişiyle karşılaşırsa 100 yeni hasta olacaktır. Binlerce hasta kişi olduğu düşünülürse artışın her gün binlerce kişiye varacağı kolayca anlaşılır
Türkiye ve İtalya Verilerinin Karşılaştırılması
Şimdi, salgından en çok etkilenen İtalya’nın corona verilerini inceleyelim ve Türkiye için tahmini bir tablo oluşturalım;
| İTALYA | TÜRKİYE | ||||
| TARİH | HASTA SAYISI | BULAŞMA
ORANI |
TARİH | HASTA SAYISI | BULAŞMA
ORANI |
| 19 ŞUBAT | 3 | 19 ŞUBAT | – | – | |
| 20 ŞUBAT | 4 | 0.75 | 20 ŞUBAT | – | – |
| 21 ŞUBAT | 21 | 4.25 | 21 ŞUBAT | – | – |
| 22 ŞUBAT | 79 | 2.76 | 22 ŞUBAT | – | – |
| 23 ŞUBAT | 157 | 0.99 | 23 ŞUBAT | – | – |
| 24 ŞUBAT | 229 | 0.46 | 24 ŞUBAT | – | – |
| 25 ŞUBAT | 323 | 0.41 | 25 ŞUBAT | – | – |
| 26 ŞUBAT | 470 | 0.46 | 26 ŞUBAT | – | – |
| 27 ŞUBAT | 655 | 0.39 | 27 ŞUBAT | – | – |
| 28 ŞUBAT | 889 | 0.36 | 28 ŞUBAT | – | – |
| 29 ŞUBAT | 1128 | 0.27 | 29 ŞUBAT | – | – |
| 1 MART | 1701 | 0.51 | 1 MART | – | – |
| 2 MART | 2036 | 0.16 | 2 MART | – | – |
| 3 MART | 2502 | 0.23 | 3 MART | – | – |
| 4 MART | 3089 | 0.23 | 4 MART | – | – |
| 5 MART | 3858 | 0.25 | 5 MART | – | – |
| 6 MART | 4636 | 0.20 | 6 MART | – | – |
| 7 MART | 5883 | 0.27 | 7 MART | – | – |
| 8 MART | 7375 | 0.25 | 8 MART | – | – |
| 9 MART | 9172 | 0.24 | 9 MART | – | – |
| 10 MART | 10149 | 0.11 | 10 MART | 1 | – |
| 11 MART | 12462 | 0.23 | 11 MART | 1 | – |
| 12 MART | 15113 | 0.21 | 12 MART | 1 | – |
| 13 MART | 17660 | 0.17 | 13 MART | 5 | 4 |
| 14 MART | 21157 | 0.20 | 14 MART | 6 | 0.20 |
| 15 MART | 24747 | 0.17 | 15 MART | 18 | 2 |
| 16 MART | 27980 | 0.13 | 16 MART | 47 | 1.611 |
| 17 MART | 31506 | 0.12 | 17 MART | 98 | 1.085 |
| 18 MART | 35717 | 0.13 | 18 MART | 191 | 0.949 |
| 19 MART | 41035 | 0.15 | 19 MART | 359 | 0.880 |
| 20 MART | 47021 | 0.15 | 20 MART | 670 | 0.866 |
| 21 MART | 53578 | 0.14 | 21 MART | 947 | 0.413 |
| 22 MART | 59138 | 0.10 | 22 MART | 1236 | 0.305 |
| 23 MART | 63927 | 0.081 | 23 MART | 1529 | 0.237 |
| 24 MART | 69176 | 0.076 | 24 MART | 1872 | 0.224 |
| 25 MART | 74386 | 0.075 | 25 MART | 2433 | 0.299 |
| 26 MART | 80589 | 0.083 | 26 MART | 3629 | 0.491 |
| 27 MART | 86498 | 0.073 | 27 MART | 5698 | 0.570 |
| 28 MART | 92472 | 0.069 | 28 MART | 7402 | 0.299 |
| 29 MART | 97689 | 0.056 | 29 MART | 9217 | 0.245 |
| 30 MART | 101739 | 0.041 | 30 MART | 10827 | 0.175 |
| 31 MART | 105792 | 0.040 | 31 MART | 13531 | 0.250 |
| 1 NİSAN | 110574 | 0.045 | 1 NİSAN | 15679 | 0.159 |
| 2 NİSAN | 115242 | 0.042 | 2 NİSAN | 18135 | 0.157 |
| 3 NİSAN | 119827 | 0.040 | 3 NİSAN | 20921 | 0.153 |
| 4 NİSAN | 124632 | 0.040 | 4 NİSAN | 23934 | 0.144 |
| 5 NİSAN | 128948 | 0.034 | 5 NİSAN | 27069 | 0.131 |
| 6 NİSAN | 132547 | 0.028 | 6 NİSAN | 30217 | 0.116 |
| 7 NİSAN | 135586 | 0.023 | 7 NİSAN | 34109 | 0.129 |
Tablo Ne Söylüyor?
Tabloda verilen skorların bazılarını inceleyelim. Örneğin 01 Mart’ta 1701 olan hasta sayısı 02 Mart’ta 2036’ya çıkmıştır. Yani bir günde 335 kişiye daha virüs bulaşmıştır. Yeni hasta sayısı olan 335’i bir önceki gündeki hasta sayısı ile oranladığımızda hastalığın bulaşma oranını o gün için tespit etmiş oluruz; 335/1701 = 0.196. Bu veri bize şu bilgiyi verir; 0 gün, enfekte olan 10 kişi 10 x 0.196 = 1.96 kişiye, 100 kişi 100 x 0.196 = 19.6 kişiye, 1000 kişi 1000 x 0.196 = 196 kişiye virüsü bulaştıracağı anlamına gelir.
İtalya’da hastalığın bulaşma oranı ve dolayısıyla yayılma hızının düşmesine rağmen hasta sayısının 130 binin üzerinde olması nedeniyle her gün üç – dört bin yeni vaka tespit edilmektedir. Yapılan test sayısı, insan bağışıklığı gibi birçok faktörün yeni vaka sayısında etkili olduğunu yazımda daha öncede belirtmiştim.
Üssel Artış İçin Projeksiyon
Ayrıca virüsün bulaşma hızındaki düşmenin 19 Mart 2020 tarihinde alınan sokağa çıkma yasağını takip eden birkaç gün içinde gerçekleşmeye başladığı görülüyor. Bir diğer sonuç ise 7 Nisan 2020 tarihi itibariyle virüsün ülkemizdeki bulaşma oranının İtalya’nın yaklaşık 6 katı olduğu görülüyor. Bu veri bize toplumsal izolasyona daha fazla dikkat etmemiz gerektiğini ve kurallara uymanın son derece gerekli olduğunu gösteriyor. Evinizde kalın, sağlıklı kalın.
Aşağıdaki tablo ülkemizde virüsün tahmini yayılması ile ilgili verileri içermektedir. Toplumsal izolasyona devam edilmesi, sağlıklı beslenme, düzenli uyku ve iyi bir psikoloji ile umuyorum ki aşağıdaki tabloya ulaşılmayacaktır.
| TARİH | HASTA SAYISI |
BULAŞMA ORANI |
| 12 NİSAN | 59042 | 0.12 |
| 17 NİSAN | 95086 | 0.1 |
| 22 NİSAN | 139709 | 0.08 |
| 1 MAYIS | 236029 | 0.06 |